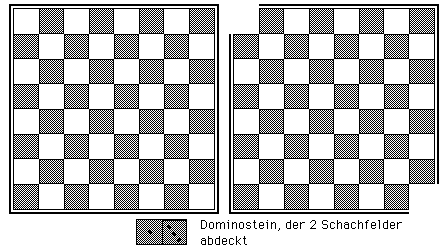
Schachbrettproblem
Ein Schachbrett hat bekanntlich 64 Felder. Es wird mit Dominosteinen abgedeckt, die je 2 Felder bedecken. Folglich kann es vollständig mit 32 Dominosteinen abgedeckt werden.

Nun kommt das Problem:
Man schneidet dem Schachbrett zwei gegenüberliegende Ecken ab (rechte Figur). Es bleiben also noch 62 Felder übrig. Wie muss man nun die 31 Dominosteine legen, damit das Schachbrett wieder vollständig abgedeckt wird?
Der Lösungsansatz für dieses Problem ist leicht anders. Nachdem ich unzählige Blätter auf der Suche nach einer Lösung gefüllt hatte, kam die Idee des Gegenbeweises. Wenn ich zeigen kann, dass es keine Lösung gibt, dann ist die Aufgabe auch gelöst. Und dieser Beweis ist in der Tat sehr einfach.
Ein Schachbrett besteht aus 64 Felder, 32 schwarze und 32 weisse. Mit einem Dominostein wird jewels ein schwarzes und ein weisses Feld belegt, ganz egal, wie man den Dominostein legt.
Werden nun zwei gegenüberliegende Ecken entfernt, dann sind dies jeweils zwei gleichfarbige Felder. Im Beispiel oben wurden 2 weisse Felder entfernt. Folglich bleiben 30 weisse und 32 schwarze Felder übrig. Diese können NICHT mit 31 Dominosteinen belegt werden. Also gibt es keine Lösung für dieses Problem.