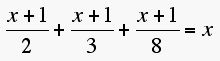
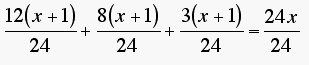
Kamelteilung
Hier die ursprünglich Kamelaufgabe, die noch etwas schwieriger zu lösen ist und mehr mathematische Kenntnisse erfordert.
Ein Kameltreiber hat 3 Söhne und will seine Kamele verteilen. Der Älteste soll die Hälfte, der Zweite einen Drittel und der Jüngste einen Achtel erhalten. Sie haben grosse Probleme bei der Aufteilung, da es nicht aufgeht. Erst als ein Beduine vorbeikommt, ihnen sein Kamel zur Teilung auslehnt, können sie dem Wunsch ihres Vaters nachkommen. Es bleibt auch ein Kamel übrig, das sie dem Beduinen wieder zurückgeben. Wie viele Kamele waren es und vieviele erhielt jeder?
Die Schwierigkeit besteht darin, dass man nicht weiss, wie viele Kamele vorhanden sind. Mit Probieren kommt man nicht weit. Erst mit Algebra und Gleichungen kommt man in nützlicher Zeit der Lösung auf die Spur. Man muss auch sehr genau notieren, was man jeweils macht.
Nicht weiterlesen, wenn du die Lösung selber herausfinden willst!
Hier mein Lösungsvorschlag:
Anzahl Kamele: x
Zur Verteilung der Kamele mit dem des Beduinen: x + 1
1. Sohn erhält: (x+1)/2 = a
2. Sohn erhält: (x+1)/3 = b
3. Sohn erhält: (x+1)/8 = c
Die Gleichung zuerst in Worten: 1.Sohn + 2.Sohn + 3.Sohn = Kamele
Und nun mathematisch: a + b + c = x
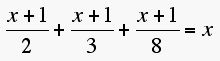
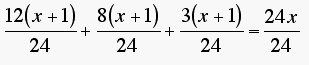
Nun multipliziert man die Gleichung mit 24 und lösst die Klammern auf.
12 x + 12 + 8 x + 8 + 3 x + 3 = 24 x
Zusammenfassen
23 x + 23 = 24 x
Nach x auflösen ergibt
x = 23
Demnach ergibt
a = (23+1)/2 = 12
b = (23+1)/3 = 8
c = (23+1)/8 = 3
12 + 8 + 3 = 23, das Kamel des Beduinen bleibt übrig und die Teilung kann gemacht werden.
Es waren 23 Kamele.
Der erste Sohn erhält 12 Kamele.
Der zweite Sohn erhält 8 Kamele.
Der dritte Sohn erhält 3 Kamele.